Jun 08, 2020
Higher Order Integral Property
Written By:
The idea of creating a distinguisher based on the HOIP is based on the following -
Idea #1
Recall the integral property of AES. We used to consider a set $P$ of $256$ plaintexts with the following properties.
$c_0$ had the All Property. $c_i$ for $0<i \leq 15$ had Constant property.
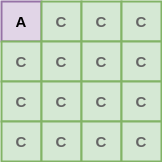
Then after applying AES 3-round on $P$ we observed the following-
$\forall$ $i$ in $0\leq i \leq15$ $c_i$ has the Balanced property.
Now consider the following: Suppose I generate 2 sets of plaintexts $P_1$ and $P_2$ according to the following rules
- In $P_1$ byte position $1$ i.e. $c_1 = 0$ while $c_0$ takes all $256$ values.
- In $P_2$ byte position $2$ i.e. $c_2 = 0$ while $c_0$ takes all $256$ values.
Now apply AES 3-round on $P_1$ and $P_2$ to obtain $C_1$ and $C_2$ ( sets of 256 ciphertexts each ) We observe that both $C_1$ and $C_2$ show Balanced property.
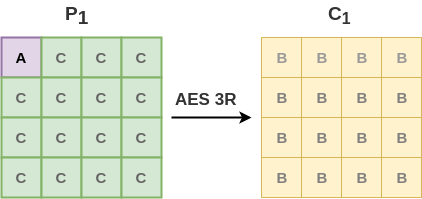
Now,
If I mix the two sets $C_1$ and $C_2$ without caring for the order, the new set $C_{12}$ of $512$ texts will still show the Balanced property.
How is this property ensured -
- $\oplus$ sum of $C_1 = 0$
- $\oplus$ sum of $C_2 = 0$
- $\implies$ $\oplus$ of $C_1 \: and \:C_2 = 0$ even without knowing which ciphertext belongs to which set.
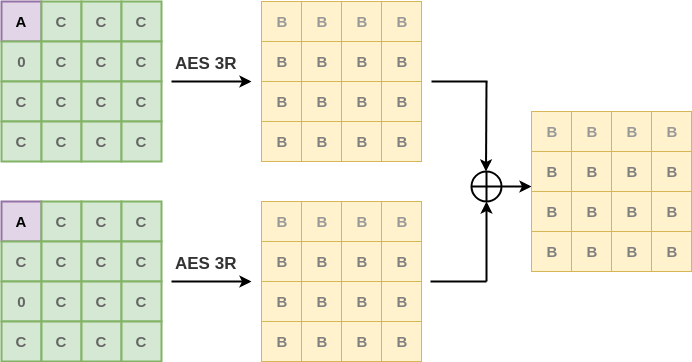
Now lets try building a distinguisher for AES 4-round
AES 4-Round Distinguisher
First things first.
What's a distinguisher ? Ideally a cipher should behave as a random output generator. However if we can find a construction which differentiates the output of a cipher from a random output, then we call it a distinguisher.
Construction
Lets first take $2^{24}$ sets of plaintexts $P_0, P_1, P_2, ...$( why ? Ill answer it later ), where each set has $256$ plaintexts. Each set is generated as follows:-
- For $P_0$ the value of $c_1 || c_2 || c_3$ is fixed to $0$, $c_0$ takes all $256$ possibilities. ($c_1, c_2$ is byte position 1 and 2 respectively)
- For $P_1$ the value of $c_1 || c_2 || c_3$ is fixed to $1$, $c_0$ takes all $256$ possibilities.
- ...
- For $P_{2^{24} - 1}$ the value of $c_1 || c_2 || c_3$ is fixed to $2^{24} - 1$, $c_0$ takes all $256$ possibilities.
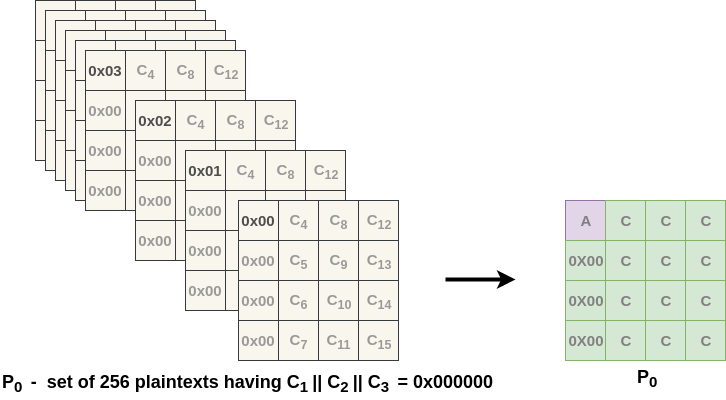
Thus total no. of plaintexts is $2^{24}. 256 = 2^{32}$
Also let $P = \{P_0, P_1,P_2, ... ,P_{2^{24}-1}\}$
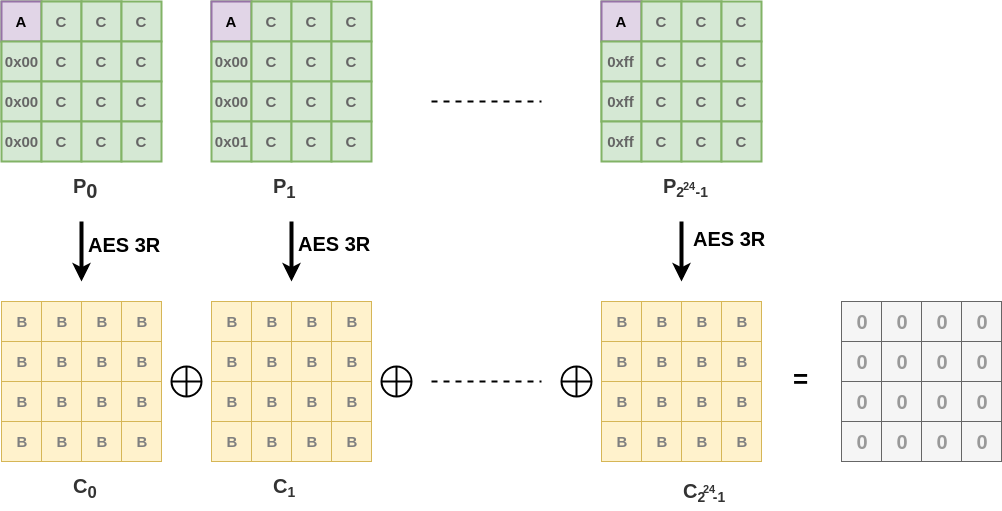
Now apply AES 3-round on all plaintexts and obtain corresponding ciphertexts. From previous discussion, each set of ciphertexts shows balanced property. Hence, the $\oplus$ sum of all $2^{24}$ sets is also $0$.
Now let's prepend one round to AES 3-round to make it 4 - rounds
Just to recap, what did we do ?
- Constructed $2^{24}$ sets of $256$ plaintexts according to some rules
- Encrypted the plaintexts using AES 3-rounds
- Mixed all of the $2^{24}$ sets together to get a set of $2^{32}$ matrices which show the balanced property ( i.e. $\oplus$ sum$=0$ )
Consider the following,
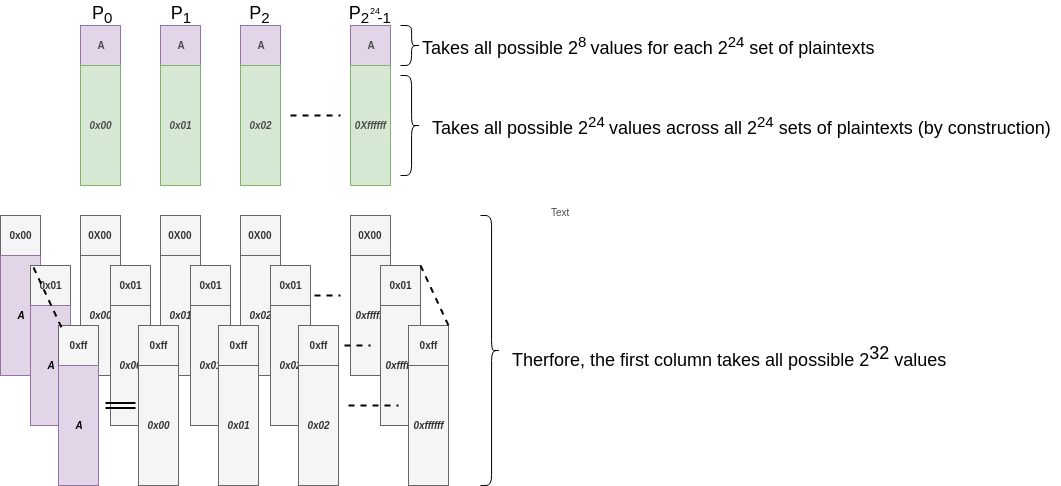
Consider all the $2^{32}$ plaintexts i.e. $P$ as $1$ set. From our construction, $c_1 || c_2 || c_3$ takes all possible values.
$c_1 || c_2 || c_3$ is 3 bytes and therefore can have $2^{24}$ distinct values. We took care of this during the construction of $P$ remember !!!
We also know that in set $P_i$, $c_0$ shows All property
Thus if we consider $c_0 || c_1 || c_2 || c_3$ ( the first column ) in $P$, it takes all possible $2^{32}$ values. And that is why we had taken $2^{24}$ sets of plaintexts in the beginning !!!
Lets take an example to understand this, Look at just the first column Corresponding to $c_0=0$ we have all $2^{24}$ values in the lower part of the column ( from the other sets ) Corresponding to $c_0=1$ we have all $2^{24}$ values in the lower part of the column ( from the other sets )
Thus as $c_0$ can take $2^{8}$ values and corresponding to each value we have $2^{24}$ values. Thus, by multiplication rule $$Total \:values = 2^8.2^{24} = 2^{32}$$
Now the distinguisher,
At this point of time we have with us $P$ which is a set of $2^{32}$ plaintexts in which the first column takes all $2^{32}$ possible values. Let us take $P$ and observe what happens to it when we compute it in the backward direction ( refer to figure )
Current State
We have the state matrix in which the first column takes all $2^{32}$ possible values. ( represented by purple color ). The fig shows the state as well as the AES round.
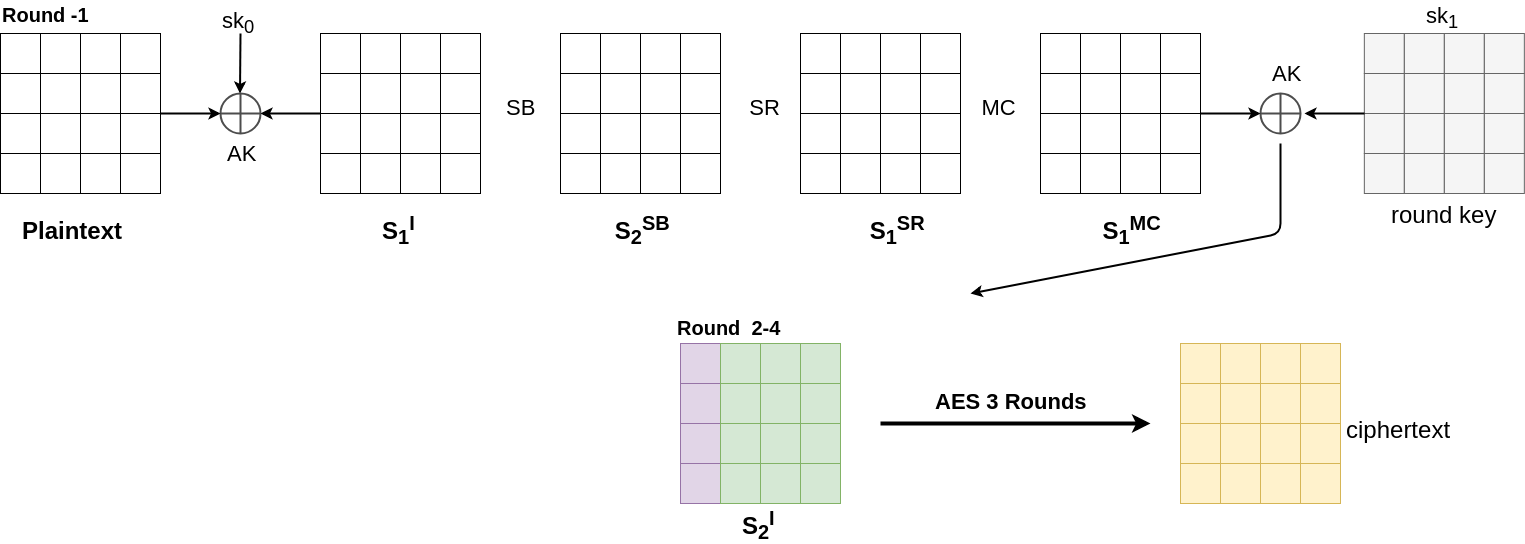
Step1. Inverse AddRoundKey
XOR does not change the structure of the state matrix as it is a bijective mapping from $byte \rightarrow byte$.
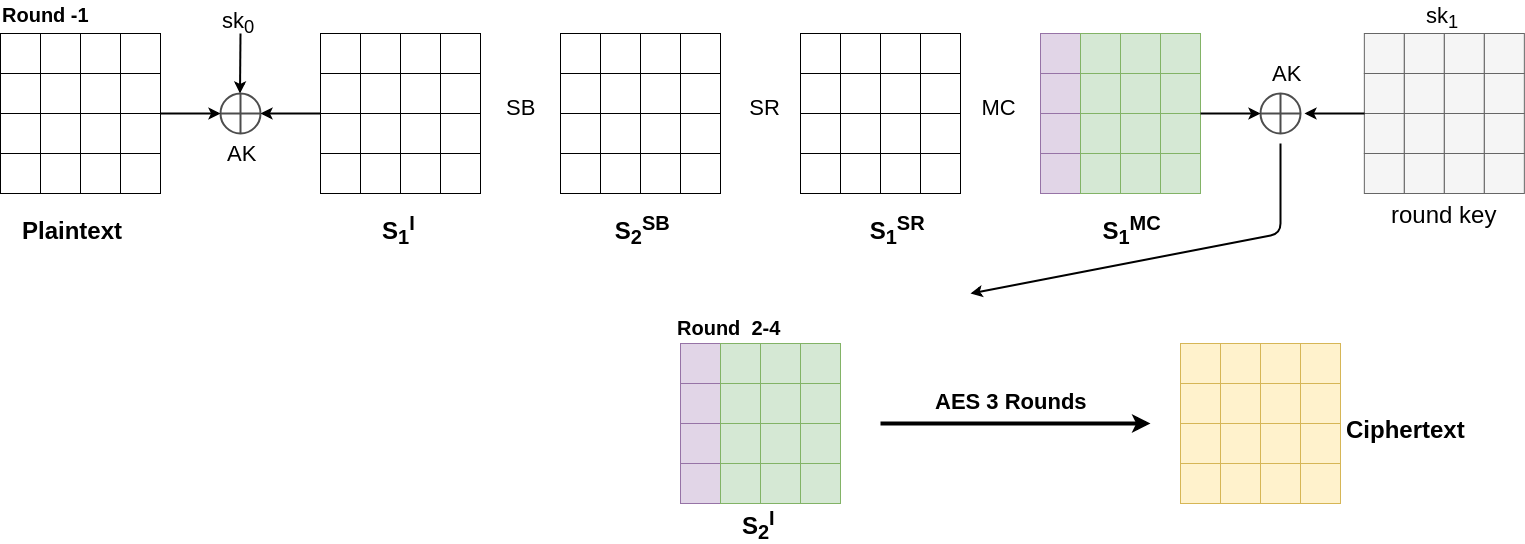
Step2. Inverse MixColumn
This too does not change the structure of the state matrix as it is a bijective mapping from $4\:bytes \rightarrow 4\:bytes$.
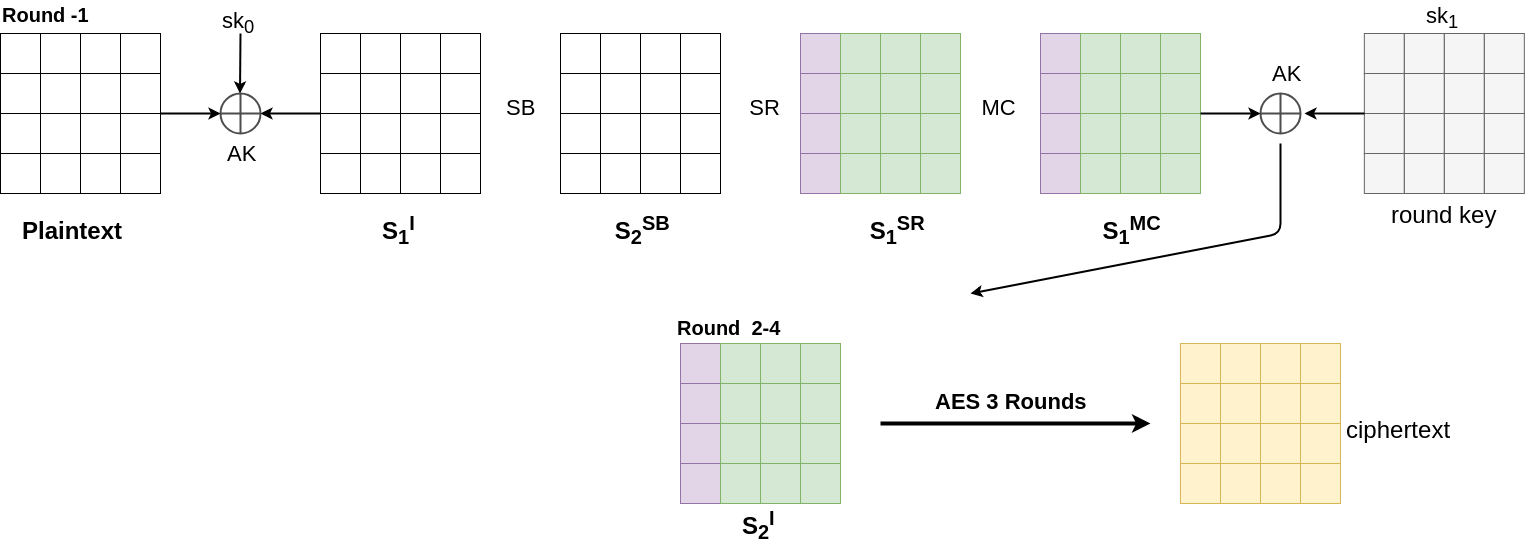
Step3. Inverse ShiftRow
This does change the structure, but as it is simply bitewise relocation, the individual property of the byte does not change.
We know that the first column takes all possible values. Since each byte in the column can have only 256 values, each value is repeated $2^{24}$ times. Thus we can say that each position in the column individually shows All property. Hence after Inverse Shift Row, individual property is preserved.
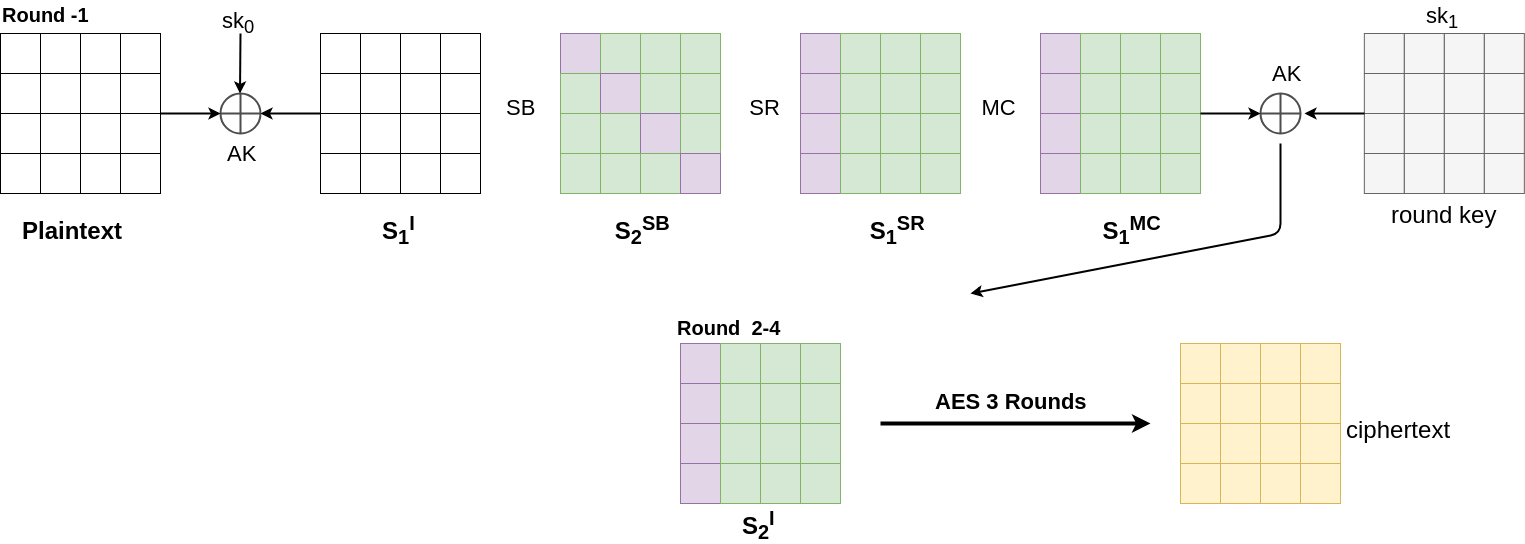
Step4. Inverse SubBytes
Again its a bijective mapping. Therefore no change in structure.
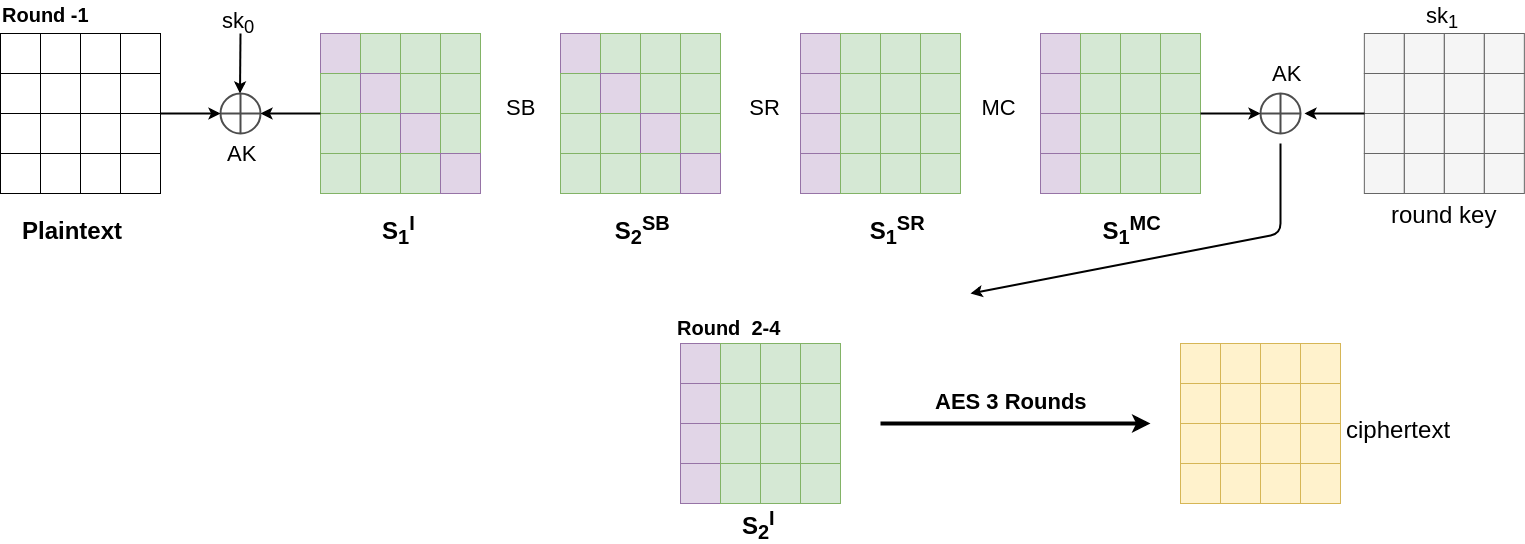
Step5. XOR with boss key
No change in structure
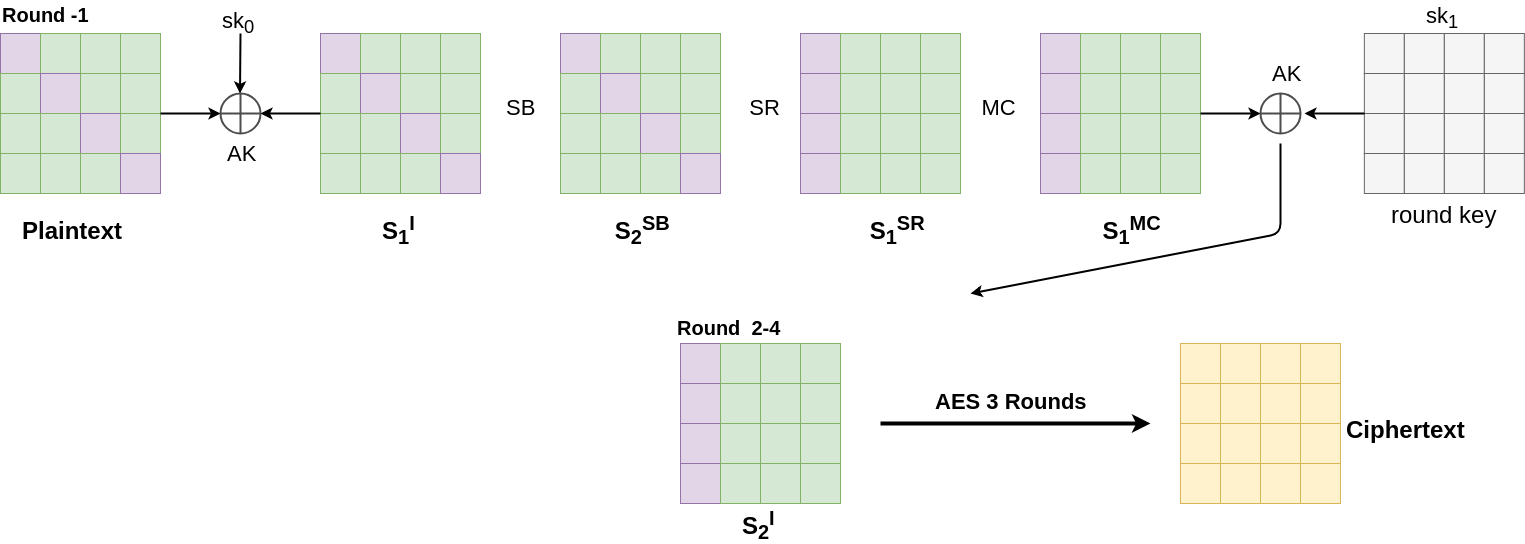
Conclusion
Now we have our distinguisher.
Let $P$ be a set of $2^{32}$ plaintexts in which the byte positions $0, 5, 10, and \:15$ take all possible values, and the other bytes take a fixed value. The corresponding $2^{32}$ states $C_0 , C_1 , . . . , C_{2^{32} −1}$ after four AES rounds have the balanced property in all the 16 bytes that is $$\bigoplus_{i=0}^{2^{32}-1}C_i[j]=0 , 0 \leq j \leq 15$$
</div> </div> </div>